Co-ordinates

08 Dec, 2023

Intro

This post looks at a fun maths-y problem I had transferring my maze display function from ASCII-art in the terminal to pixels and points in Nannou's window.

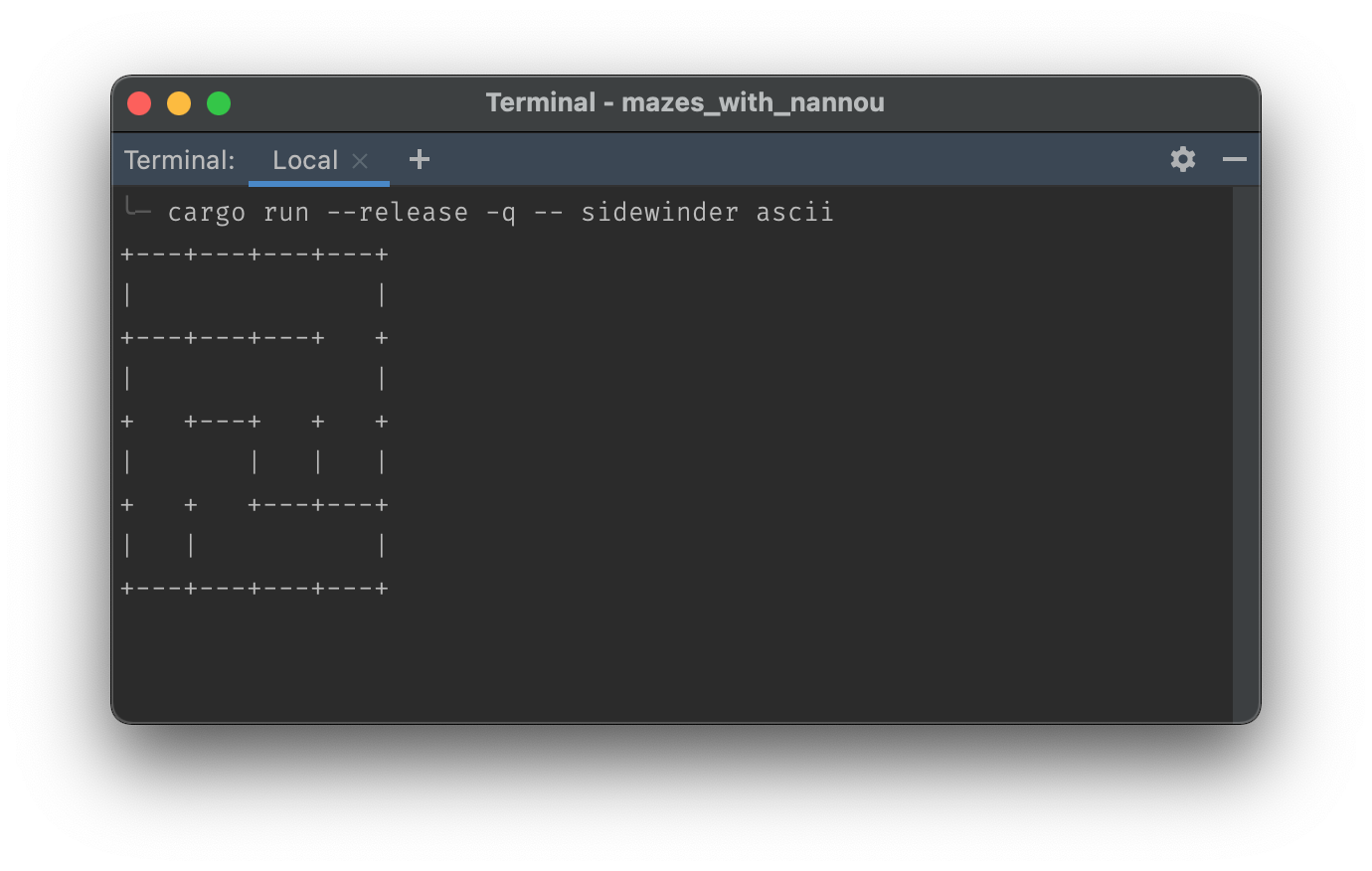
My starting point, displaying a maze using ASCII characters and the terminal:

Where I wanted to get to, displaying a maze using pixels and Nannou:

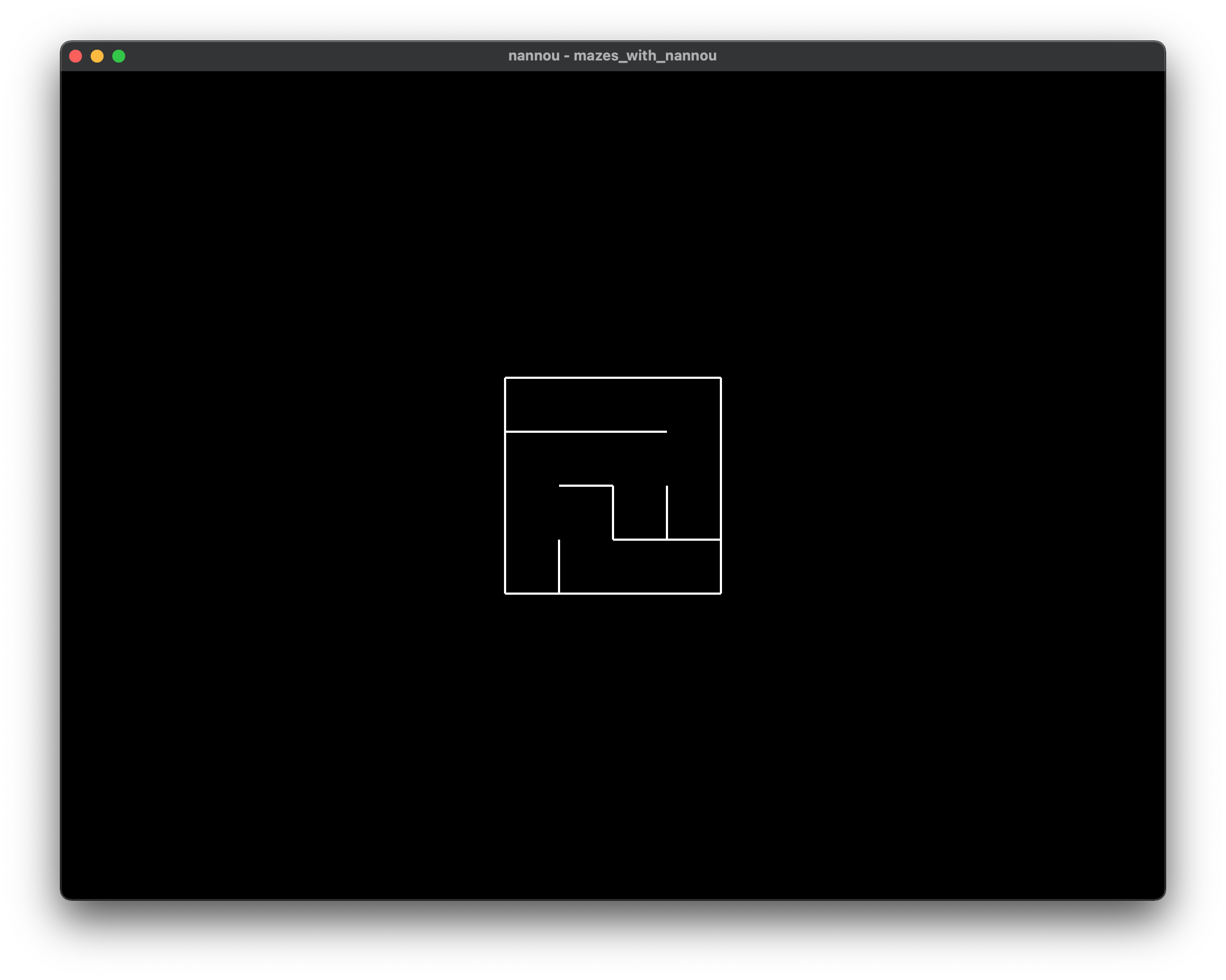
(To more clearly illustrate the problem, I'm using a small, hardcoded, sidewinder maze (which I still need to add entrances to...). You can see the code for it it here).

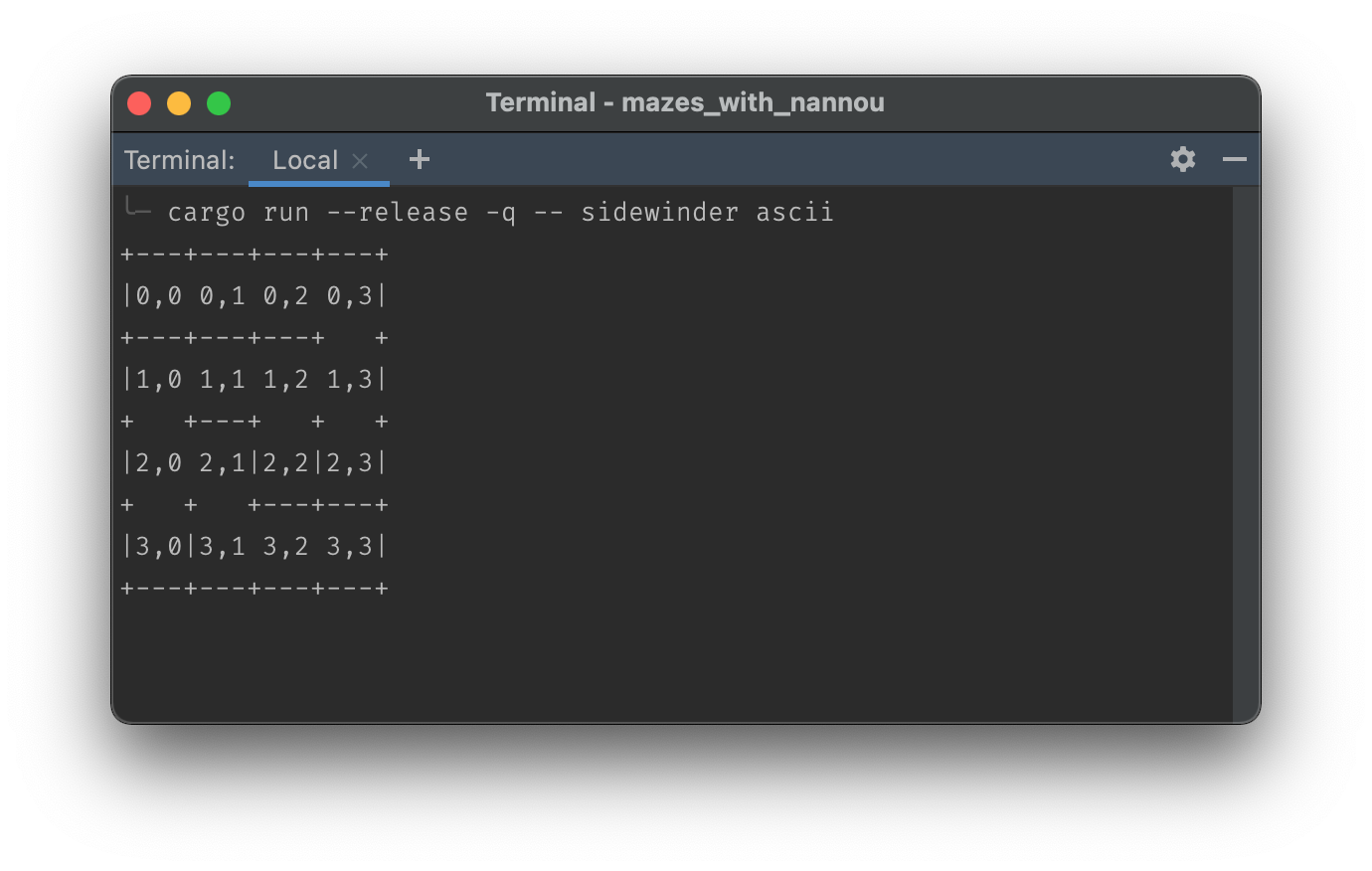
An ASCII maze

This is what I started with, the mazes produced using my cli_display() function.

Displaying the maze left-aligned in ASCII-space is fairly straightforward:

• The first cell in the first vector, with vector indices of 0,0, appears in the top left.
• There is no need to do any calculations on where to output each subsequent cell, the indexing does everything for you

(Full code here)

To be able to display the maze outside the terminal and in Nannou's window, I needed to move to pixels and points instead of ASCII characters and Cartesian-space instead of Shell-space.

Moving to a Nannou maze

I chose Nannou because I was at Recurse Center at the time and all the people on the creative coding group were singing the praises of Nannou as a creative coding framework for those interested in Rust.

Moving to Nannou meant moving to a Cartesian co-ordinate system.

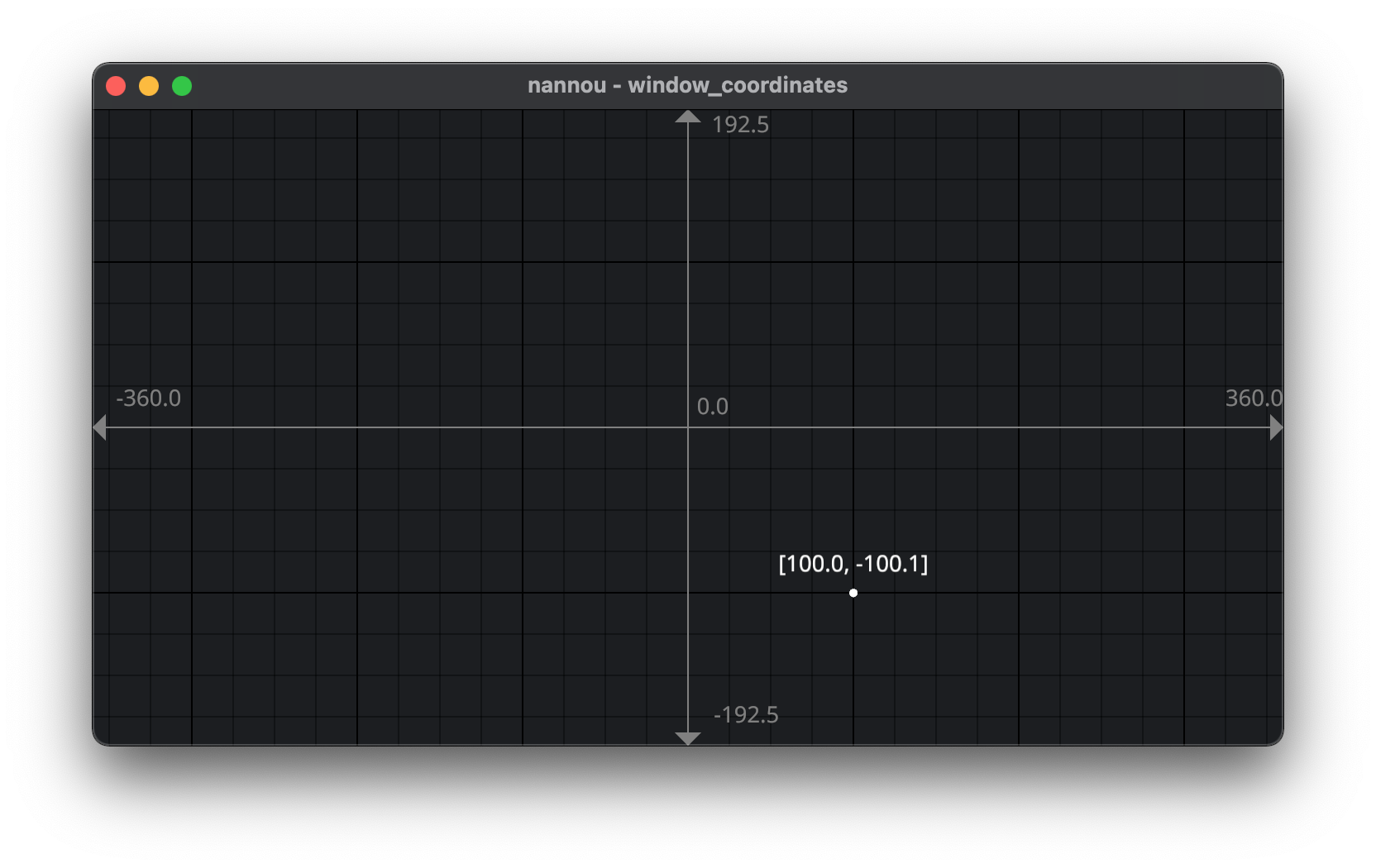
In a Cartesian system 0,0 is at the center, and there are positive and negative numbers on each axes:

What I expected

I had expected to move from this ASCII output:

To this pixel output (x (red) and y (yellow) axes and grid superimposed for clarity):

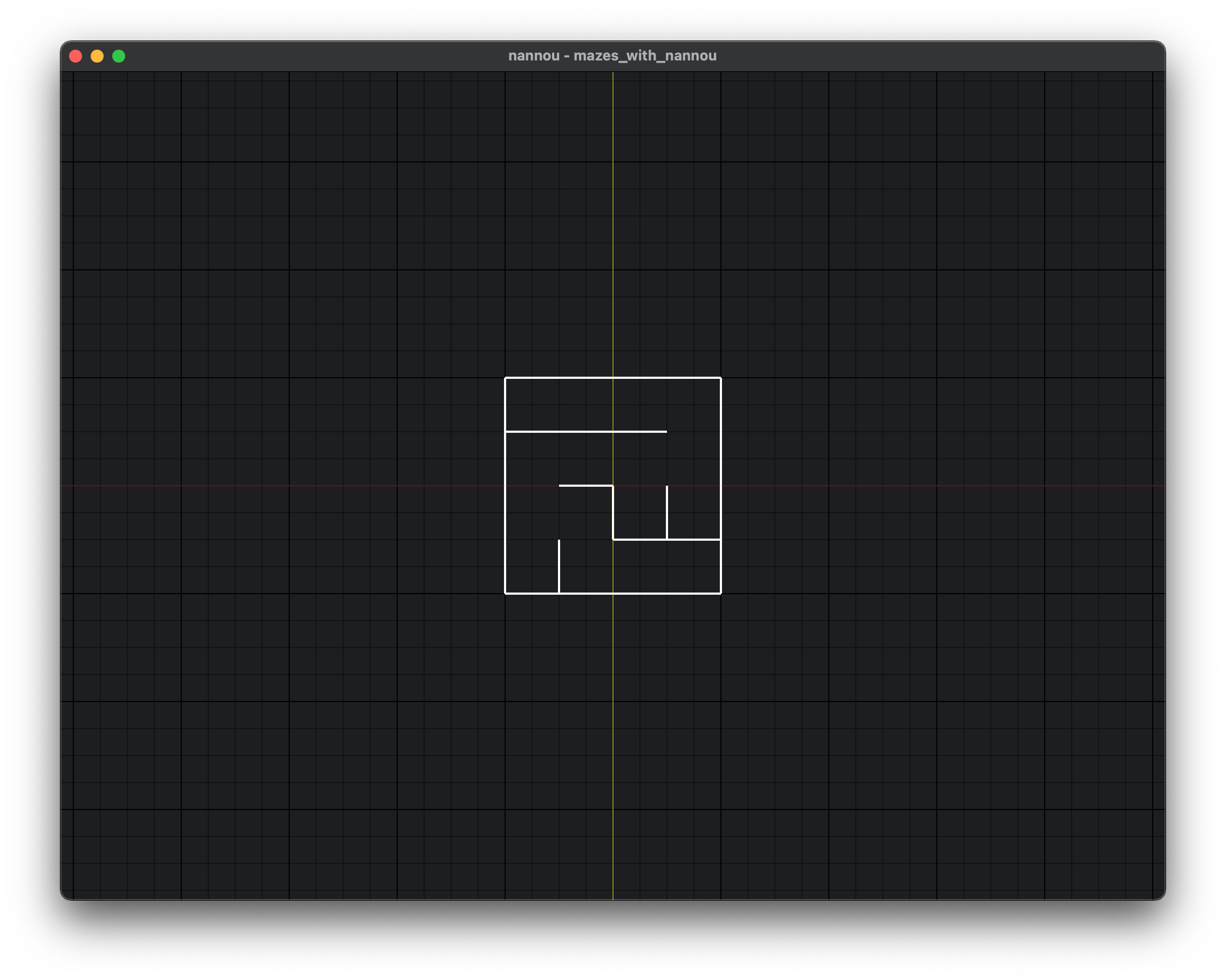
What I got

Instead, my maze looked like this:

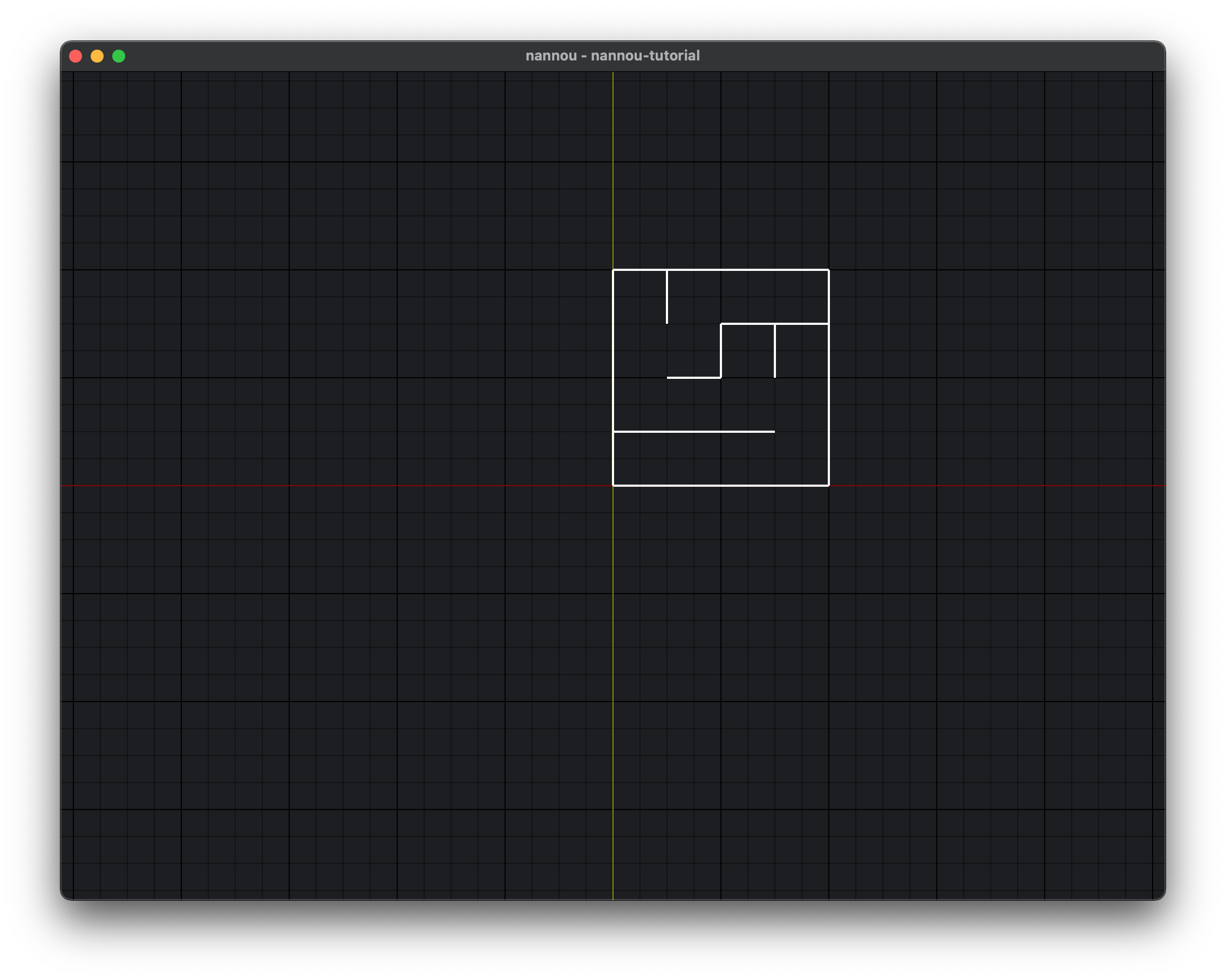
Why?

This happened because I wasn't really thinking about a key difference: :

• 0,0 in Shell-space appears in the top left
• 0,0 in Cartesian-space appears in the centre.

In other words, I had directly (and therefore incorrectly) mapped the each maze cell's indices to Cartesian x y co-ordinates.

The structure of the maze is a nested vector, so the first cell in the first vector with indices 0,0 would start in the center of the display because those I was treating those indices as x y co-ordinates.

To illustrate, here is our original ASCII maze, with each cell also outputting its vector indices:

You can see that:

• The first number, that of the vector's index in the outer vector, increments from top to bottom of the display.
• The second number, that of the cell's index in the inner vector, increments from left to right of the display.

In comparison here is the same Nannou maze also outputting its vector indices:

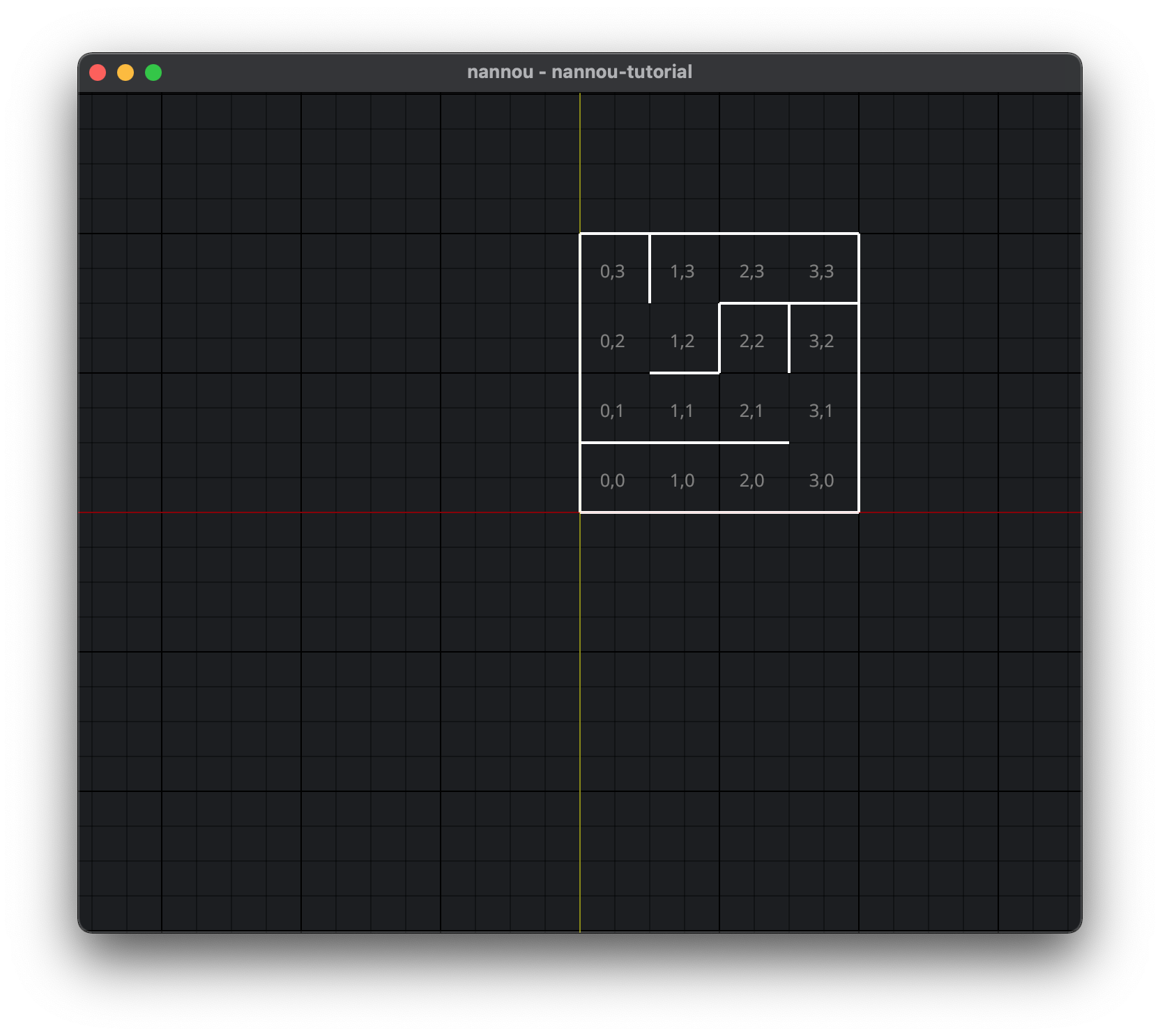
The same cells are located very differently when the cell indices are used implicitly in shell-space versus their explicit use as xy co-ordinates in Cartesian space:

• The first number, which is now doubling as the x co-ordinate, increments from left to right of the display. Previously it was from top to bottom.
• The second number, now doubling as the y co-ordinate, increments from bottom to top of the display. Previously it was from left to right.

What should the code have done instead?

The code needed to do two things:

1. Calculate how to center the maze i.e. where to start the first cell
2. Calculate how to orientate the maze i.e. where to place all subsequent cells after first cell

One of the main reasons I'm writing this up is because I managed to do it, but I really struggled to explain to myself, in simple terms, what the problem was and how I solved it.

So I'm writing this up here, to help consolidate that process further.

1. Calculate how to center a square maze

We want to know where to start drawing a maze, such that this origin ensures the maze is horizontally and vertically centered.

Steps to calculate maze origin:

1. Get maze size (number of inner vectors and cells per vector) e.g. 4 x 4
2. Get maze cell size e.g. 10px
3. Halve the maze size and times by the cell size e.g. 2 * 10 = 20
4. Invert this number to get the x co-ordinate e.g. -20
5. Keep this number to get the y co-ordinate e.g. 20
6. This x,y pair of -20, 20 now represent the maze origin i.e. the co-ordintes of the top left point of the first cell

Or, if we say X and Y represent x and y co-ordinates for the maze's origin, we can put it as:

• c = number of columns / maze width / number of cells per inner vector
• r = number of rows / maze height / number of inner vectors
• s = cell size i.e. number of pixels assigned to a cell's width and height

X = -( c / 2 ) * s
Y = ( r / 2 ) * s Where:

2. Calculate how to orientate the maze

We've seen how to start the maze, but where to go from there? What about the next cell we want to draw? And the one after that?

Part of the problem of the initial implementation was that the starting point of subsequent cells were calculated by naively incrementing both the x and y co-ordinates using addition.

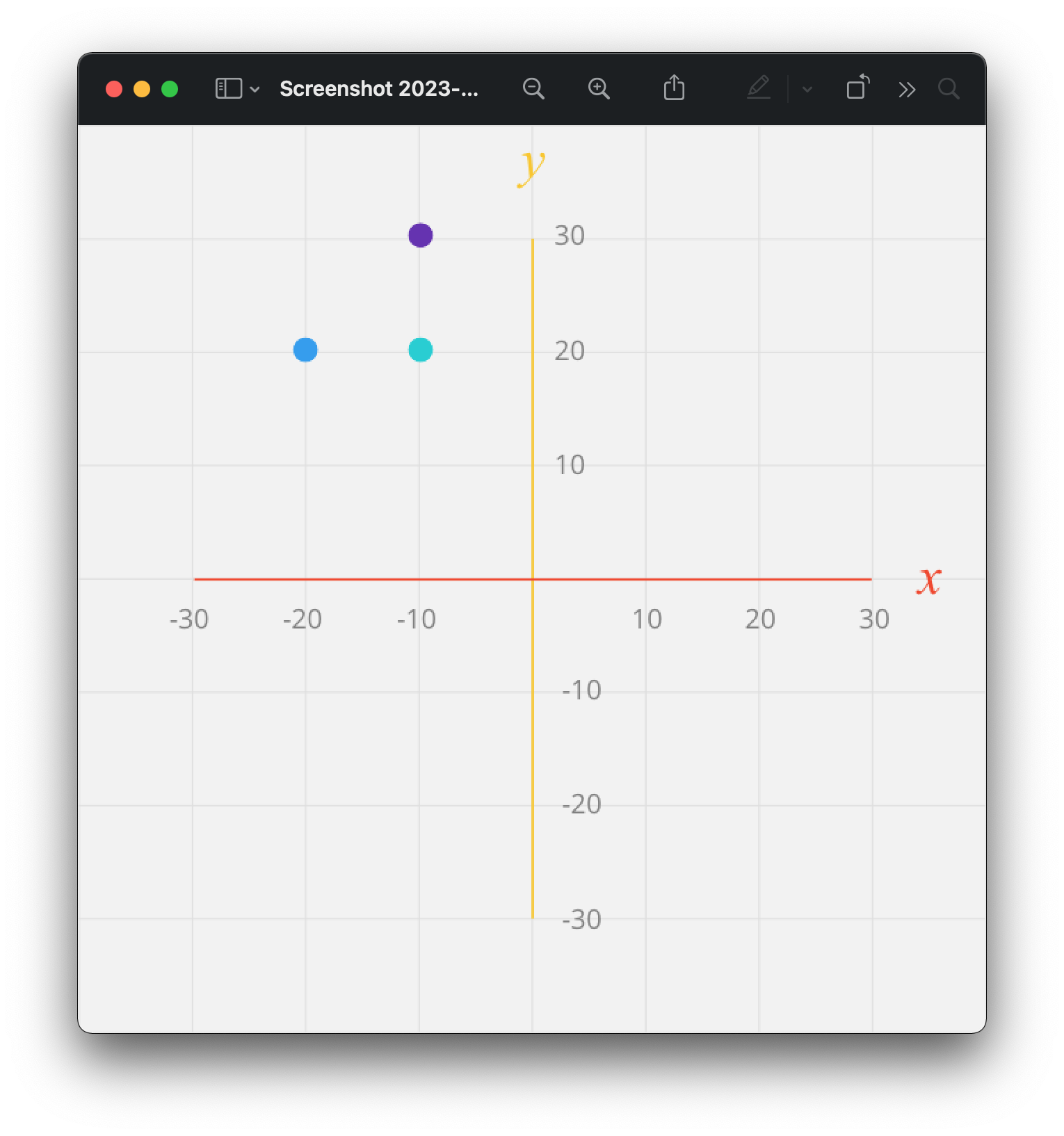
But this is not what we want to do:

• say your maze origin x y co-ordinates have been calculated as -20, 20 (blue dot)
• therefore you want the subsequent cell's origin to be -10, 20 (cyan dot)
• but if you are incrementing by addition to both x y co-ordinates, you'll calculate the next cell's origin as -10, 30 (purple dot)

Instead, what we need to do is this:

1. Take the maze origin x y co-ordinates e.g. -20, 20
2. Take the current cell's vector indices e.g. 0, 1
   1. The first index is taken as the y co-ordinate
   2. The second index as x co-ordinate
3. Calculate the x y steps by multiplying these indices by the cell size e.g.
   1. y step is produced by 0 * 10 = 0
   2. x step is produced by 1 * 10 = 10
4. For the current cell's x origin co-ordinate, add the maze origin x co-ordinate to the x step e.g. -20 + 10 = -10
   1. For the current cell's y origin co-ordinate, subtract the y step from the maze origin y co-ordinate e.g. 20 - 0 = 20

If we say that x' and y' represent the x and y cell origin co-ordinates that we're trying to calculate, then we can express the above steps as the formulae:

x’ = X + x
y’ = Y - y

Where:

• X = x value of maze's origin co-ordinates

• x = index of current cell's location in its inner vector And:

• Y = y value of maze's origin co-ordinates

• y = index of current cell's vector's location in the outer vector

Show me the code

This is what the eventual Rust code looked like to implement these formulae:

let x_index = cell.location.column;
let x_origin = &_model.origin.x;
let cell_size = &_model.cell_size;
let current_x_origin = x_origin + (x_index as f32 * cell_size).floor();

let y_index = cell.location.row;
let y_origin = &_model.origin.y;
let size = &_model.cell_size;
let current_y_origin = y_origin - (y_index as f32 * size).floor();

let north_west_point = pt2(current_x_origin, current_y_origin);
let north_east_point = pt2(
  (current_x_origin + cell_size).floor(),
  current_y_origin
);
let south_east_point = pt2(
  (current_x_origin + cell_size).floor(),
  (current_y_origin - cell_size).floor(),
);
let south_west_point = pt2(
  current_x_origin,
  (current_y_origin - cell_size).floor()
);